在数学中,当我们说腐(x) = 无限大时,意味着函数在接近某个特定的值x时,其值将无限增长,通常表示为腐(x) → ∞。这种行为在数学分析和图形学中经常出现,需根据具体背景进行详细讨论。

当我们说腐(x) = 无限大时,实际上是在讨论函数的极限。极限是函数在某一点附近的表现,如果当自变量x趋向于某个值时,函数的值趋近于无限大,我们就说腐(x) = 无限大。这种情况可能表明函数在这一点附近没有定义,或者存在一个垂直渐近线。
腐函数通常与有理函数有关,例如当分母趋于0而分子不为0时,函数的值会趋向于无限大。一个简单的例子是f(x) = 1/x^2,在x=0时,函数趋于无限大,可以表示为lim(x→0) 1/x^2 = ∞。
在图形学中,腐(x) = 无限大可能表示函数在某个点存在一个垂直渐近线,函数在该点附近呈现无穷增长的趋势。这对于绘制图形以及理解函数的行为具有重要意义。
腐(x) = 无限大是数学中一个重要的概念,在不同的上下文中具有不同的解释和应用。理解腐函数的性质有助于我们深入研究函数的行为,并在数学建模、工程领域以及图形学中应用这些概念。

在足球的世界里,球星们不仅是场上的英雄,也是公众人物,他们的行为举止...
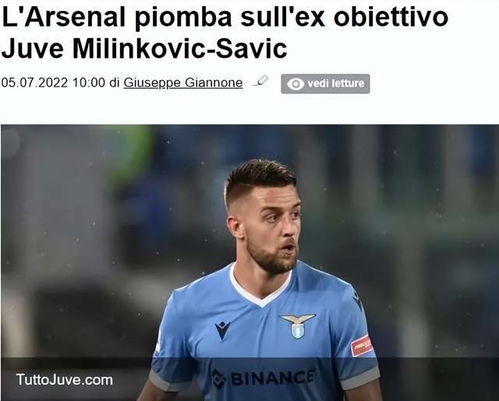
直播吧9月12日讯拉齐奥主帅巴罗尼接受了媒体的采访,对球队新援、阿森...

直播吧9月20日讯本轮中超北京国安客场3-1战胜梅州客家。第88分钟...

都说穷则思变,早就烂到根上的中国男足在世预赛遭遇耻辱性连败之后,对人...

北京时间9月23号,陈梦解锁“校长”身份,孙颖莎王楚钦也有新身份,马...